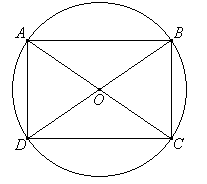El teorema de Thales dice que el �ngulo A es recto, pues est� inscrito en una semicircunferencia.	Thales pudiera haber usado esta figura para demostrar el teorema.

Sir Thomas L. Heath, en su libro Greek Mathematics aventura que Thales pod�a haber demostrado el teorema razonando de la siguiente manera sobre la figura del rect�ngulo ABCD:

Como en los tri�ngulos ADC, BCD, los lados AD, DC son iguales a BC, CD respectivamente, y los �ngulos comprendidos (ambos rectos) son iguales, los tri�ngulos son iguales en todos los aspectos. Por tanto, el �ngulo ACD (o sea,  OCD) es igual al �ngulo BDC (o sea, ODC). De aqu� se deduce, por el rec�proco de la proposici�n 5 del Libro I de los Elementos de Euclides, conocido por Thales, que OC = OD. De forma similar se podr�a demostrar que OD=OA. Por tanto, OA, OD, OC (y OB) son todos iguales, y una circunferencia con centor O y centro OA pasar�a por B, C y D. Ahora, AOC, por ser una linea recta, es un di�metro de la circunferencia y ADC es una semicircunferencia. El �ngulo ADC es un �ngulo inscrito en una circunferencia y es recto por hip�tesis.

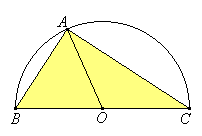Como OA y OB son iguales, los �ngulos ABO y BOA tambi�n son iguales y como OA y OC son iguales, los �ngulos OAC y OCA son iguales. Por tanto, BAC es la suma de ABC y ACB. Teniendo en cuenta que la suma de los tres �ngulos de un tri�ngulo BAC debe ser recto.

P�gina principal